SAFARI integrates the Lazy Abstraction paradigm with a symbolic backward reachability analysis.

The architecture of the tool is schematically represented by the following picture, and each module is described in detail in [1].

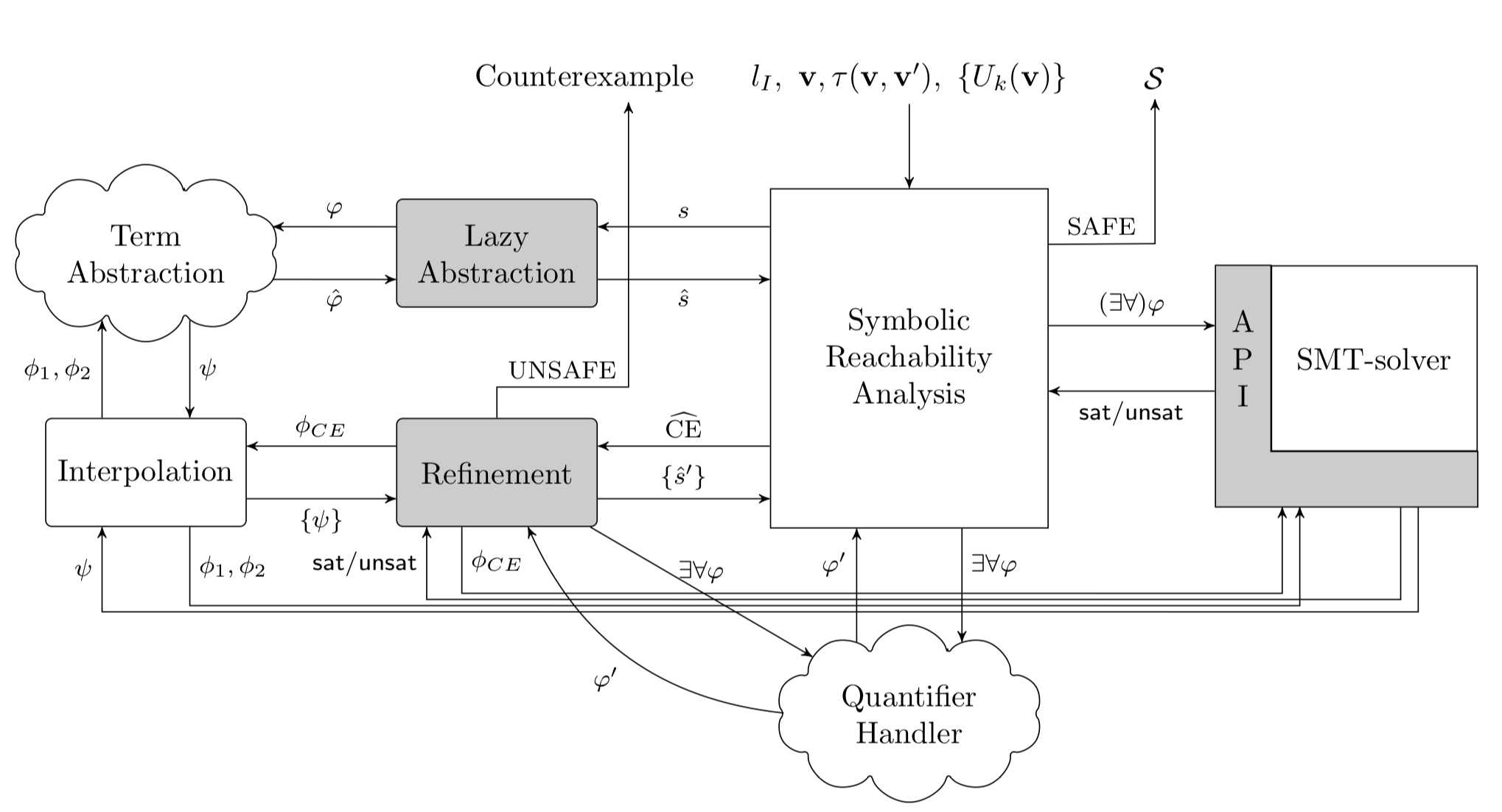
The input code represents a transition system (see the Tutorial section for more information about input syntax). The backward reachability analysis explores the state (abstract) state space. In the case of counterexamples, SAFARI generates a formula that is satisfiable if the counterexample can be reproduced by the concrete model. Otherwise, the abstract model is refined by means of interpolation.

Given the presence of quantifiers in the transition relation, in order to refine the abstract model, SAFARI generates an equisatisfiable quantifier-free formula from the counterexample, and from this formula, interpolants are computed. Interpolants are then conjoined with formulae labeling nodes on the spurious path.

If the input transition system is UNSAFE, i.e., it is possible to reach from a state satisfying I(v) one of the formulae U(v), SAFARI returns a counterexample, stating which transition has been applied, and identifying for each transition on which INDEX variable has been identified the quantified variables of the transition (if any). See the Tutorial section for more information on reading the counterexamples returned by SAFARI. On the other hand, if the system is SAFE, SAFARI returns a safe inductive invariant, i.e., a collection of universally quantified formulae representing an overapproximation of the reachable state space non intersecting with any of the U(v) formulae. This section describes how to exploit the safe inductive invariant returned by SAFARI in Floyd-Hoare proofs.

References